688. В начало строя!
Капрал Студип
любит командовать своим отрядом. Его любимый приказ “в начало строя”. Он
выстраивает свой отряд в шеренгу и оглашает последовательность приказов. Каждый
приказ имеет вид “Солдаты с li
по ri – в начало строя!”.
Пронумеруем
солдат в начальном положении с 1 до n,
слева направо. Приказ “Солдаты с li
по ri – в начало строя!”
означает, что солдаты, стоящие с li
по ri включительно
перемещаются в начало строя, сохраняя относительный порядок.
Например, если в
некоторый момент солдаты стоят в порядке 2, 3, 6, 1, 5, 4, после приказа
“Солдаты с 2 по 4 – в начало строя!” порядок будет 3, 6, 1, 2, 5, 4.
По данной
последовательности приказов найти конечный порядок солдат в строю.
Вход. В первой строке два целых числа n и m
(2 ≤ n ≤ 100 000, 1
≤ m ≤ 100 000) –
количество солдат и количество приказов. Следующие m строк содержат по два целых числа li и ri
(1 ≤ li ≤ ri ≤ n).
Выход. Выведите
n целых чисел – порядок солдат в
конечном положении после выполнения всех приказов.
|
Пример входа |
Пример выхода |
|
6 3 2 4 3 5 2 2 |
1 4 5
2 3 6 |
РЕШЕНИЕ
структуры
данных – декартово дерево, неявный ключ
Анализ алгоритма
Для решения задачи используем декартово дерево с неявным
ключом. Введем в структуру вершины Item дополнительное
поле Value. Оно будет содержать номер
солдата в строю. Создадим декартово дерево, на i-ое место (нумеруются с нуля) поставив вершину со значением Value = i + 1.
Далее выполняем команды капрала при помощи функций Merge и
Split. Вырезаем из декартового дерева отрезок [li, ri] и ставим его в начало.
Пример
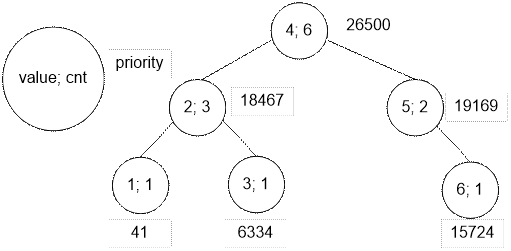
В примере в
строю находится n = 6 солдат. Сначала создадим декартово
дерево с неявными ключами 1, 2, 3, 4, 5, 6. Приоритеты выбираем случайными. В переменной value храним номер солдата в
текущей вершине.
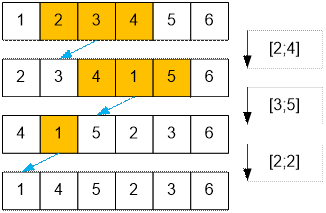
Промоделируем
процесс выполнения команд капрала.
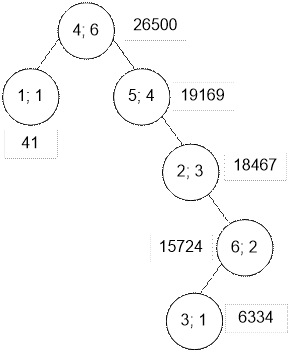
Конечное
состояние дерева:
Реализация алгоритма
Структура
вершины Item имеет
следующий вид.
struct Item
{
int cnt,
Value, Priority;
Item *l, *r;
Item() { }
Item (int
Priority, int Value) : Priority(Priority),
Value(Value),
l(NULL),
r(NULL) { }
};
Функция PrintTree выводит содержимое декартового дерева.
void PrintTree(Pitem t)
{
if (!t) return;
PrintTree(t->l);
printf ("%d",t->Value);
PrintTree(t->r);
}
На позицию pos декартового
дерева t вставляем вершину it.
void Insert (Pitem &t, Pitem it, int pos)
{
Pitem t1,t2;
Split(t,t1,t2,pos);
Merge(t1,it,t1);
Merge(t1,t2,t);
}
Основная часть программы. Создадим декартово дерево с неявным
ключом. Поскольку изначально солдаты в строю пронумерованы последовательно от 1
до n, то занесем в поле Value вершин дерева значения от 1 до n.
scanf("%d %d",&n,&m);
for(i = 0; i < n; i++)
Insert(Tree,new
Item(rand(),i+1),i);
Последовательно выполняем команды
капрала. Следует вырезать из декартового дерева отрезок [li, ri] при помощи функции Split и поставить его в начало используя
Merge.
for(i = 0; i < m; i++)
{
scanf("%d
%d",&l,&r);
Split(Tree,Tb,Tc,r);
Split(Tb,Ta,Tb,l-1); //
Tree = (Ta, Tb, Tc)
Merge(Tb,Ta,Tree); // Ta, Tb, Tc -> Tb, Ta, Tc
Merge(Tree,Tc,Tree); //
Tree = (Tb, Ta, Tc)
}
Выводим порядок солдат в конечном положении
после выполнения всех приказов.
PrintTree(Tree); printf("\n");